The Rhombus Problem

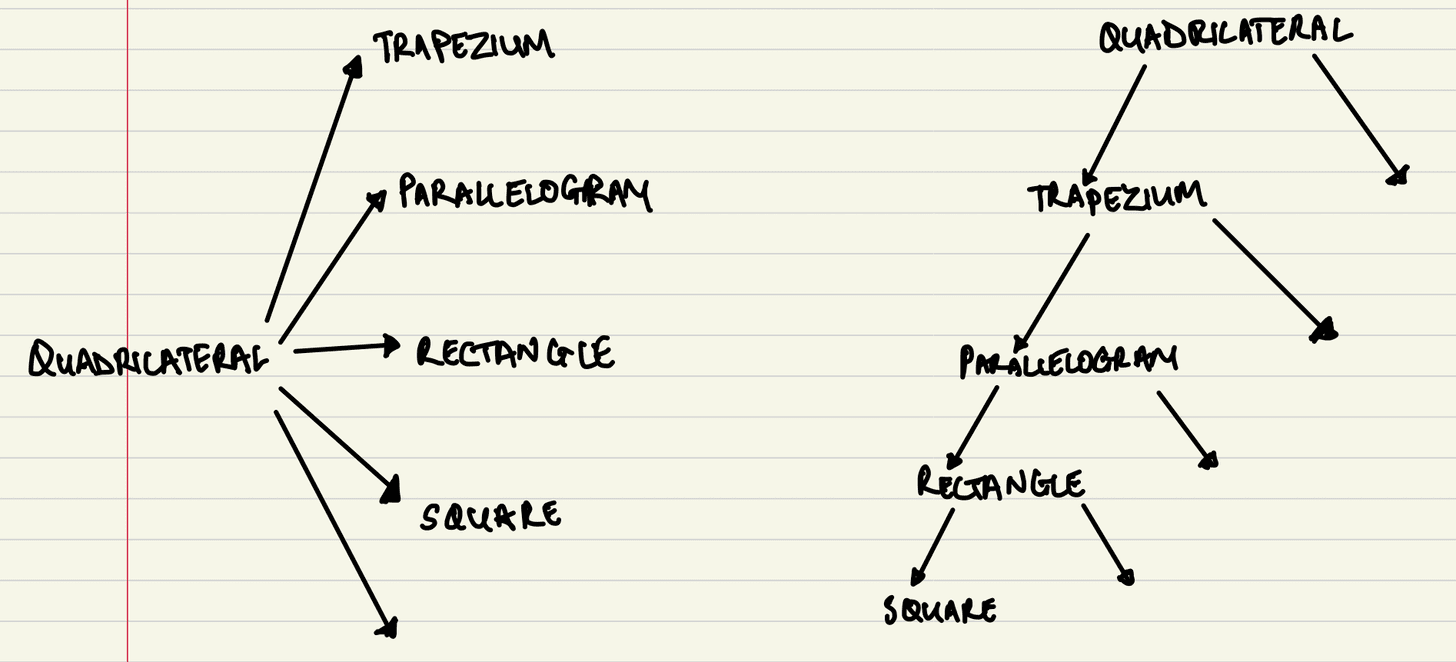
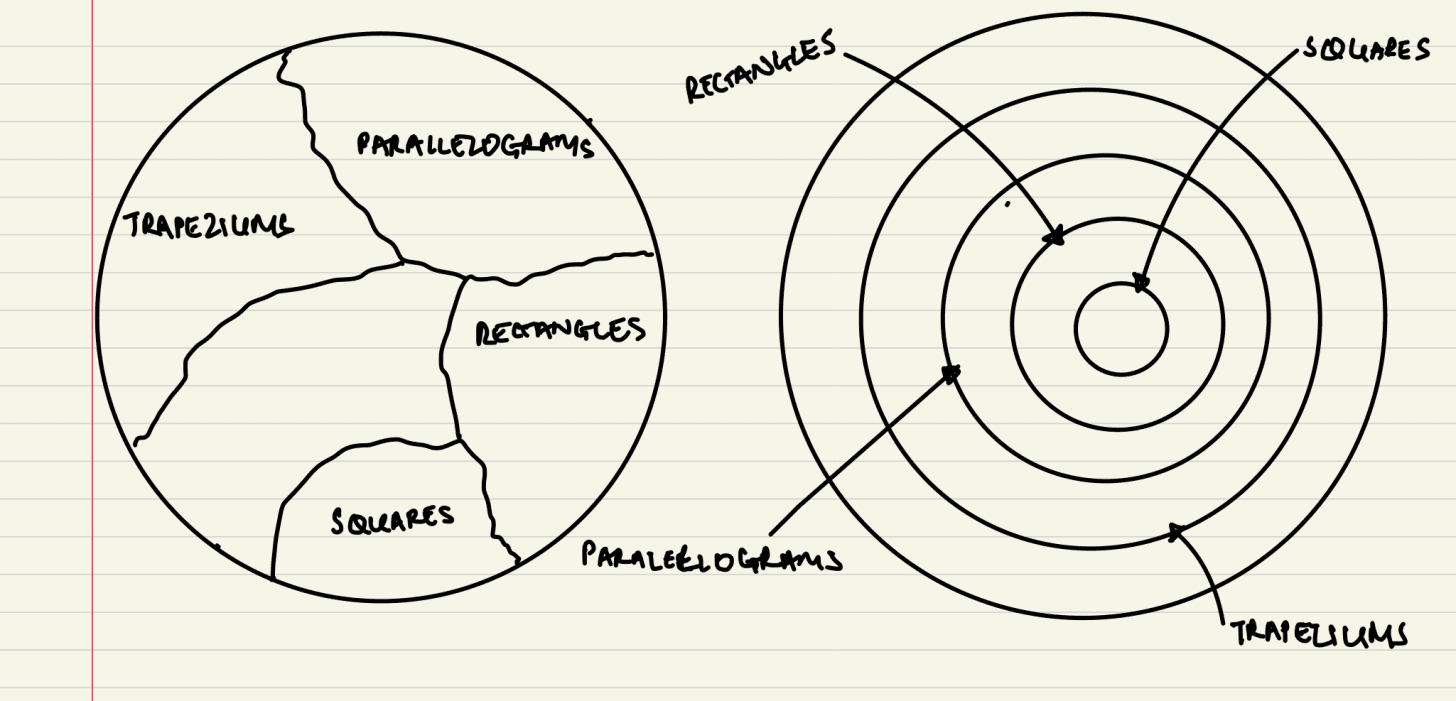
Lagard tried to add rhombuses to both systems. The globe system was straightforward — rhombuses simply became another separate category.

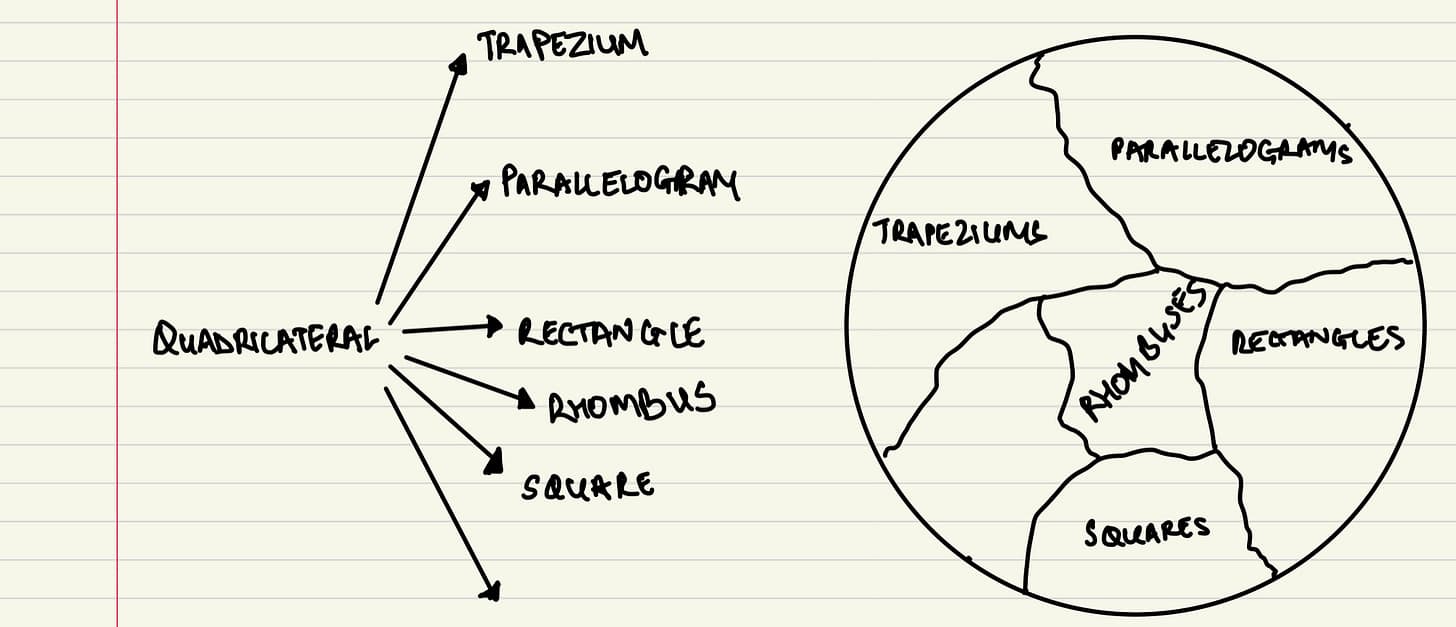
But the skyscraper system was a problem. Squares are both rectangles AND rhombuses, yet not all rectangles are rhombuses, and not all rhombuses are rectangles. In a tree, each shape can only have one "parent." A square can't sit under both rectangle and rhombus simultaneously.

Lagard figured out a way to handle this in the Venn diagram version — overlapping circles for rectangles and rhombuses, with squares in the intersection:

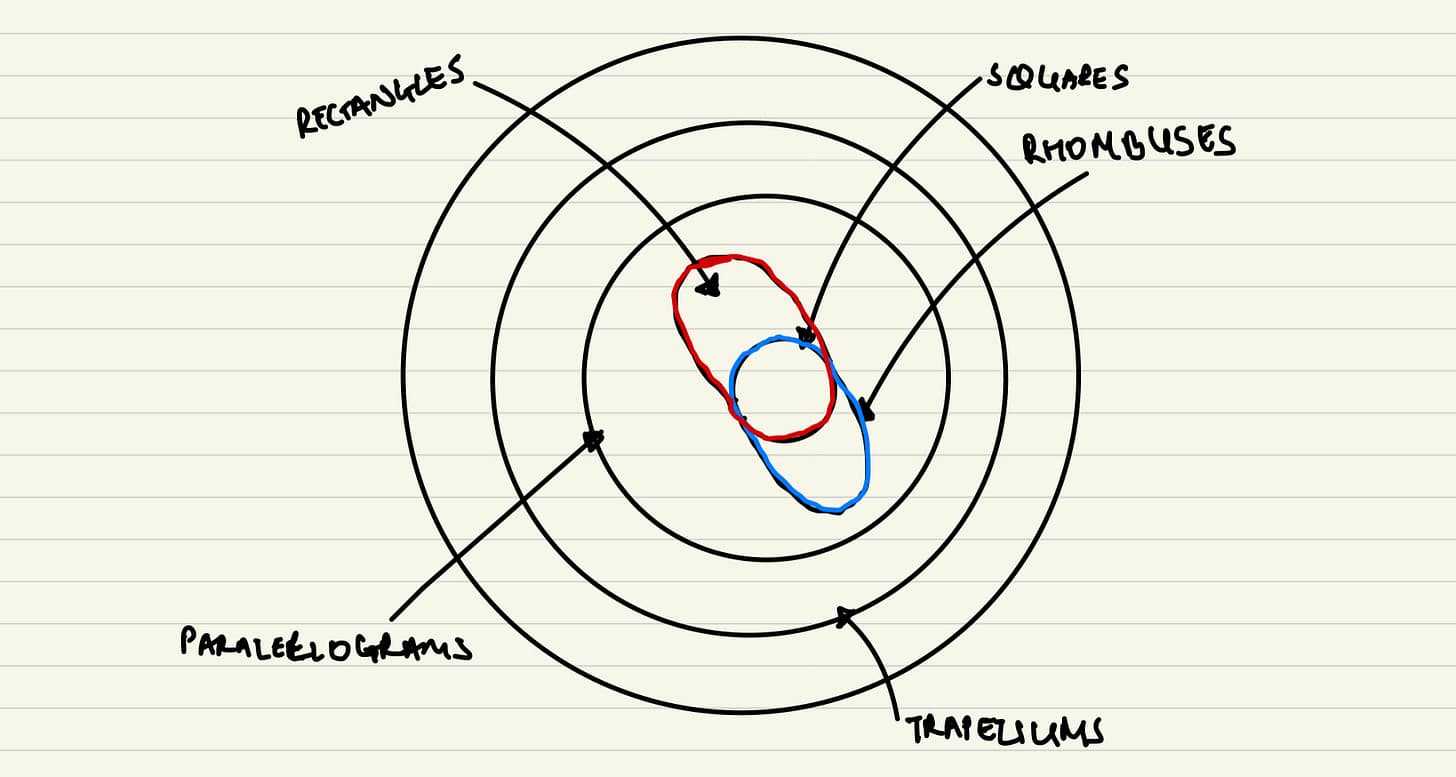
Glagalbagal's Solution

But the tree version still seemed impossible. When Fliba consulted her sister Glagalbagal, she provided a solution: a modified diagram that's no longer technically a "tree" but rather has a shape that can have two parents. In graph theory, this is called a directed acyclic graph, or DAG — though Glagalbagal wisely did not burden Fliba and Lagard with that term.

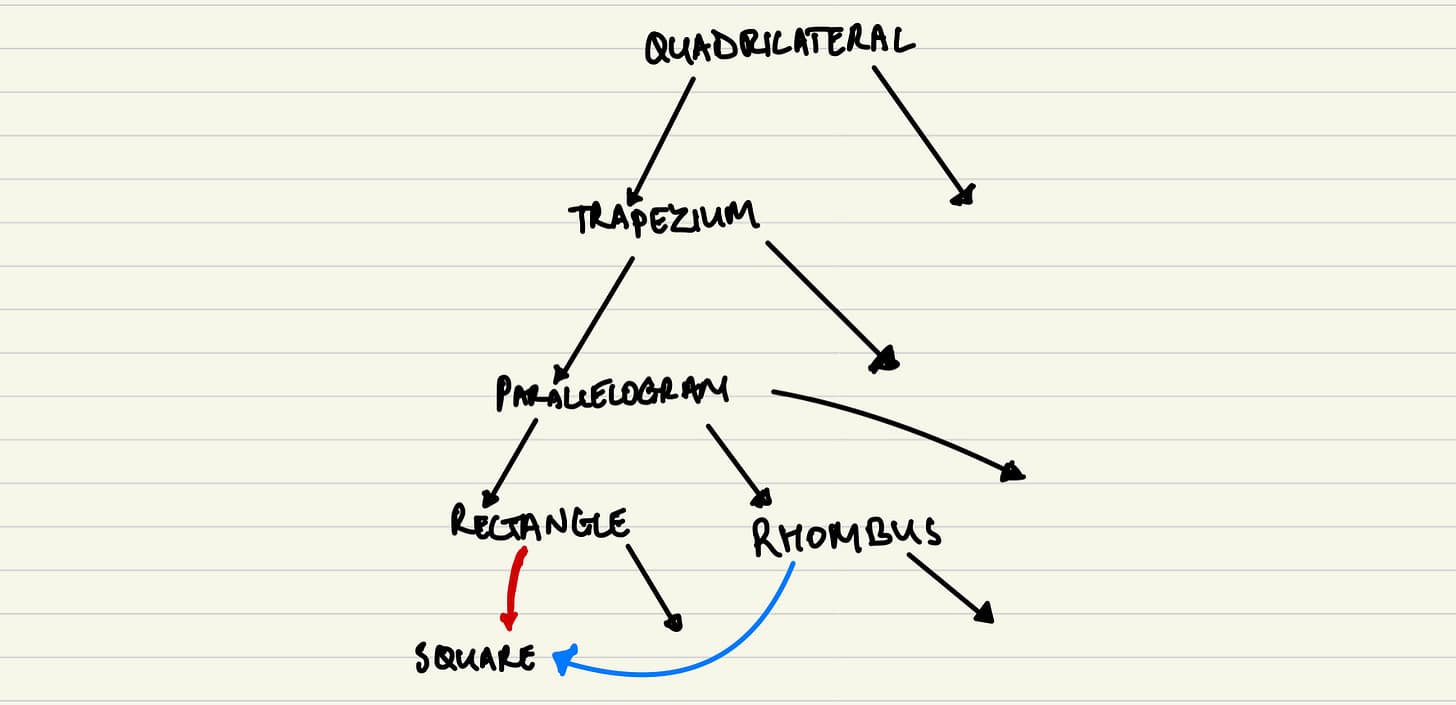
In this diagram, the square has arrows pointing to it from both rectangle and rhombus, showing that it is a type of both.

The Definitions Compared

For the globe system, they had to revise multiple definitions when adding rhombuses:

• Parallelogram: opposite sides parallel, unequal sides, and non-right angles
• Rhombus: all sides equal, not all right angles

For the skyscraper system, adding a rhombus required just one clean definition: A rhombus is a parallelogram with all sides equal.

The critical realisation came next: a rhombus with 90-degree angles is mathematically identical to a rectangle with equal sides — both are squares. The skyscraper system captures this elegantly; the globe system has to awkwardly exclude it from multiple categories.

Lagard: I’m convinced. The skyscraper system is better — even though the diagram is slightly more complex, the definitions are dramatically simpler. And every time you add a new shape, the globe system forces you to go back and redefine existing shapes. The skyscraper system just slots the new shape in.